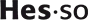Très abstraite, la géométrie hyperbolique a permis récemment le développement d’applications concrètes. Les explications du professeur de mathématiques Matthieu Jacquemet.
TEXTE | Maxime Garcia
Deux droites parallèles qui se coupent. Impossible, direz-vous? Dans la géométrie euclidienne, celle que l’on apprend classiquement à l’école, c’est effectivement inimaginable. Mais dans la géométrie hyperbolique, une infinité de droites «parallèles» peuvent se couper en un même point. Découverte au début du XIXe siècle, cette discipline mathématique a longtemps été considérée comme une théorie abstraite. Depuis quelques années, elle mène au développement de nombreuses applications. Professeur associé de mathématiques à l’Institut systèmes industriels de la HES-SO Valais-Wallis, Matthieu Jacquemet se réjouit du fourmillement qui entoure actuellement cette discipline.

Alors que la géométrie hyperbolique a été découverte au XIXe siècle, des applications concrètes commencent seulement à émerger. Comment expliquer que deux siècles aient été nécessaires pour passer de la théorie à la pratique?
La géométrie hyperbolique est passée pendant deux cents ans pour une jolie théorie abstraite qui «ne sert à rien». Puis dans les années 1980, deux grands mathématiciens ont contribué à faire prendre conscience de son importance. D’abord Bill Thurston, lauréat de la médaille Fields en 1982, a montré que la géométrie hyperbolique était bien plus centrale qu’on ne le pensait jusqu’alors – elle est même la plus riche des trois géométries à courbure constante (lire encadré p. 33). Ensuite, en utilisant d’autres approches, le mathématicien Mikhaïl Gromov a apporté des innovations importantes montrant que la géométrie hyperbolique possède des ramifications multiples. Suite à ces travaux, les gens ont commencé à comprendre que des applications étaient possibles. Mais entre le moment où les «matheux» ont réalisé que la géométrie hyperbolique n’était pas seulement une curiosité théorique et le moment où on a pu l’utiliser effectivement, il a fallu un temps de «digestion» par la communauté, ainsi qu’un temps de «diffusion» vers les autres domaines scientifiques. C’est pourquoi toutes les applications concrètes de la géométrie hyperbolique sont relativement récentes. Aujourd’hui, ce domaine est en plein boom.
Quelles sont ses principales applications?
L’utilisation de la géométrie hyperbolique est particulièrement prometteuse dans le contexte des réseaux complexes, qui surviennent eux-mêmes dans de multiples disciplines (ingénierie, informatique, communication, biologie, sociologie, etc.). Elle est notamment utilisée pour étudier des modèles proie-prédateur dans la chaîne alimentaire, la modélisation des connexions cérébrales, le développement de modèles de deep learning, ou dans les réseaux électriques. Cela est dû au fait qu’un graphe (une collection de points reliés par un certain nombre de connexions) est intrinsèquement un objet de type hyperbolique.

Dans le domaine de la visualisation de données (mapping), l’espace hyperbolique (visualisé à l’aide du disque de Poincaré1Le disque de Poincaré (nommé en l’honneur du mathématicien français Henri Poincaré (1854-1912) est un modèle de géométrie hyperbolique construit à partir des points intérieurs à un disque. Le bord de ce disque est appelé «cercle limite». On y appelle «droites» les arcs de cercles orthogonaux au cercle unité.) est intéressant pour représenter les hiérarchies de manière efficace. Concrètement, c’est un peu comme si, dans une photo, toutes les informations avaient une taille inversement proportionnelle à leur distance par rapport au centre: lorsque vous zoomez sur un personnage situé à l’arrière-plan, celui-ci passe au centre de l’image et devient net.

L’espace hyperbolique reste abstrait. Comment l’expliquer simplement?
Une selle de cheval, qui est courbée négativement, est un des exemples les plus simples. De plus, tout le monde a déjà observé la géométrie hyperbolique, notamment dans les arts. La fameuse oeuvre Circle Limit IV de Escher est ainsi une représentation de l’espace hyperbolique, en l’occurrence du disque de Poincaré.
À l’école, les enfants apprennent principalement, pour ne pas dire uniquement, la géométrie euclidienne. La découverte des années plus tard qu’il existe d’autres géométries crée un «pluralisme théorique». Est-ce problématique?
Les mathématiques enseignées à l’école obligatoire ont été découvertes au plus tard au Moyen Âge, ce qui peut donner l’impression que «tout a été inventé». Pourtant, les mathématiques n’ont jamais cessé de se développer; elles n’ont même jamais été aussi foisonnantes qu’actuellement ! En ce qui concerne la géométrie, il existe plusieurs géométries «différentes». Ce n’est pas un problème, car ces théories ne sont pas concurrentes. Elles se complètent, apportent chacune de la richesse, car chacune a pour origine un point de vue ou un contexte différents.
La géométrie euclidienne est restée pendant vingt siècles la seule et l’unique. Pourquoi a-t-il fallu autant de temps pour dépasser cette théorie ?
Les mathématiques existent depuis que l’humanité existe. Au départ, les gens faisaient de la géométrie en fonction de ce qu’ils voyaient autour d’eux. Vers 300 ans avant J.-C., le mathématicien grec Euclide a matérialisé les connaissances en formulant cinq axiomes. Dès le départ, le cinquième axiome, qui dit en substance que deux droites parallèles ne se coupent jamais, semblait un peu à part, car plus complexe que les autres. Pendant les siècles suivants, les mathématiciens ont «buté dessus» en essayant de prouver qu’il découlait des quatre axiomes précédents.
Au XIXe siècle, enfin, des mathématiciens ont découvert que l’on pouvait tout simplement supprimer le cinquième axiome, en gardant les quatre autres. Cela a donné naissance à des théories cohérentes: les géométries sphérique et hyperbolique. Pourquoi est-ce arrivé au XIXe siècle? Peut-être que c’est un héritage des Lumières. Comme les autres scientifiques, les mathématiciens ont commencé à réfléchir de manière abstraite, sans rester cantonnés dans ce qu’ils pouvaient voir. Cela étant dit, s’il a fallu attendre le XIXe siècle pour que la géométrie sphérique soit formalisée mathématiquement, les navigateurs l’utilisaient déjà depuis longtemps. Sur Terre, par exemple, la distance la plus courte entre deux points du globe n’est pas une ligne droite comme dans la géométrie euclidienne. C’est un arc de cercle.
Les trois géométries à courbure constante
Euclidienne – courbure nulle C’est la géométrie la plus connue, celle que l’on apprend à l’école. Parmi ses caractéristiques, deux droites parallèles ne se coupent jamais et la somme des angles d’un triangle est égale à 180°.
Sphérique – courbure positive Il s’agit du modèle le plus simple de géométrie non euclidienne, puisqu’il suffit de se représenter la Terre pour la comprendre. Concrètement, deux parallèles, à l’image des méridiens aux pôles Nord et Sud, se coupent systématiquement et la somme des angles d’un triangle est toujours supérieure à 180°. La géométrie sphérique a des applications pratiques importantes, notamment en navigation et en astronomie.
Hyperbolique – courbure négative L’espace hyperbolique n’est pas plat ni bombé, mais courbé «vers l’intérieur», comme une selle de cheval. Par un point extérieur à une droite passent une infinité de parallèles, et la somme des angles est toujours inférieure à 180°.